In-memory Search
Napkin friends, from near and far, it’s time for napkin problem number 6!
As always, consult sirupsen/napkin-math to solve today’s problem, which has all the resources you need. Keep in mind that with napkin problems you always have to make your own assumptions about the shape of the problem.
Problem 6
Quick napkin calculations are helpful to iterate through simple, naive solutions and see whether they might be feasible. If they are, it can often speed up development drastically.
Consider building a search function for your personal website which currently doesn’t depend on any external services. Do you need one, or can you do something ultra-simple, like loading all articles into memory and searching them with Javascript? Can NYT do it?
Feel free to reply with your answer, would love to hear them! Mine will be given in the next edition.
Answer is available in the next edition.
Answer to Problem 5
The question is explained in depth in the past edition. Please refresh your memory on that first! This is one of my favourite problems in the newsletter so far, so I highly recommend working through it — even if you’re just doing it with my answer below.
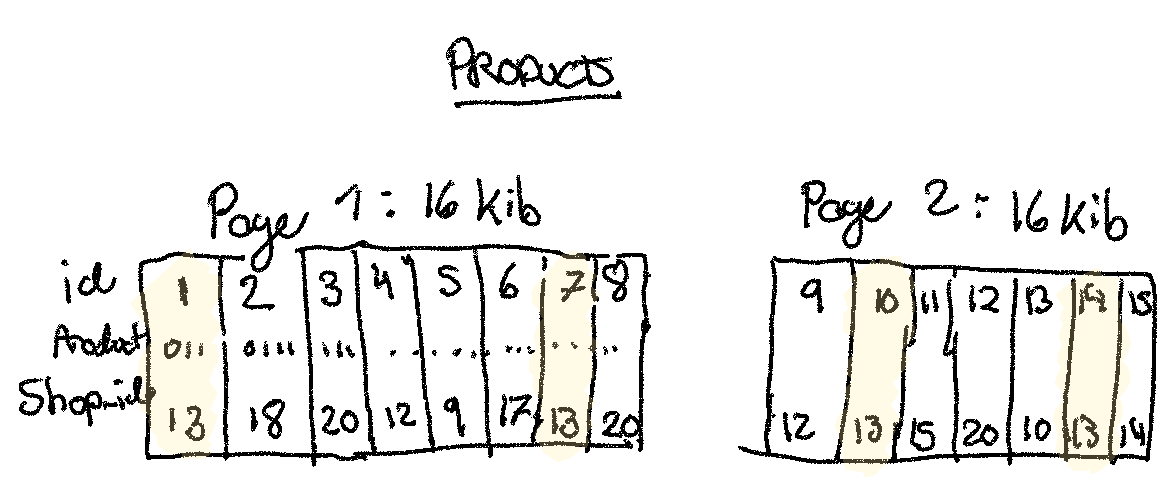
(1) When each 16 KiB database page has only 1 relevant row per page, what is the
query performance (with a LIMIT 100)?
This would require 100 random SSD access, which we know from the
resource to be 100 us each, so a total of 10ms for this simple query
where we have to fetch a full page for each of the 100 rows.
(2) What is the performance of (1) when all the pages are in memory?
We can essentially assume sequential memory read performance for the 16Kb page,
which gets us to (16 KiB / 64 bytes) * 5 ns =~ 1250 ns. This is certainly an
upper-bound, since we likely won’t have the traverse the whole page in memory.
Let’s round it to 1 us, giving us a total query time of 100 us or 0.1ms,
or about 100x faster than (1).
In reality, I’ve observed this many times where a query will show up in the slow query log, but subsequent runs will be up to 100x faster, for exactly this reason. The solution to avoid this is to change the primary key, which we can now get into…
(3) What is the performance of this query if we change the primary key to
(shop_id, id) to avoid the worst case of a product per page?
Let’s assume each product is ~128 bytes, so we can fit 16 Kib / 128 bytes = 2^14 bytes / 2^7 bytes = 2^7 = 128 products per page, which means we only need
a single read.
If it’s on disk, 100 us, and in memory (per our answer to (2)) around 1 us.
In both cases, we improve the worst case by 100x by choosing a good primary key.
You might also like...