Redis throughput
Napkin friends, from near and far, it’s time for napkin problem number four! If you are wondering why you’re receiving this email, you likely watched my talk on napkin math and decided to sign up for some monthly training.
Since last, there has been some smaller updates to the napkin-math repository and the accompanying program. I’ve been brushing up on x86 to ensure that the base-rates truly represent the upper-bound, which will require some smaller changes. The numbers are unlikely to change by an order of magnitude, but I am dedicated to make sure they are optimum. If you’d like to help with providing some napkin calculations, I’d love contributions around serialization (JSON, YAML, …) and compression (Gzip, Snappy, …). I am also working on turning all my notes from the above talk into a long, long blog post.
With that out of the way, we’ll do a slightly easier problem than last week this week! As always, consult sirupsen/napkin-math for resources and help to solve today’s problem.
Napkin Problem 4
Today, as you were preparing you organic, high-mountain Taiwanese oolong in the kitchennette, one of your lovely co-workers mentioned that they were looking at adding more Redises because it was maxing out at 10,000 commands per second which they were trending aggressively towards. You asked them how they were using it (were they running some obscure O(n) command?). They’d BPF-probes to determine that it was all GET <key> and SET <key> <value>. They also confirmed all the values were about or less than 64 bytes. For those unfamiliar with Redis, it’s a single-threaded in-memory key-value store written in C.
Unphased after this encounter, you walk to the window. You look out and sip your high-mountain Taiwanese oolong. As you stare at yet another condominium building being built—it hits you. 10,000 commands per second. 10,000. Isn’t that abysmally low? Shouldn’t something that’s fundamentally ‘just’ doing random memory reads and writes over an established TCP session be able to do more?
What kind of throughput might we be able to expect for a single-thread, as an absolute upper-bound if we disregard I/O? What if we include I/O (and assume it’s blocking each command), so it’s akin to a simple TCP server? Based on that result, would you say that they have more investigation to do before adding more servers?
Solution to this problem is available in the next edition
Answer to Problem 3
You can read the problem in the archive, here.
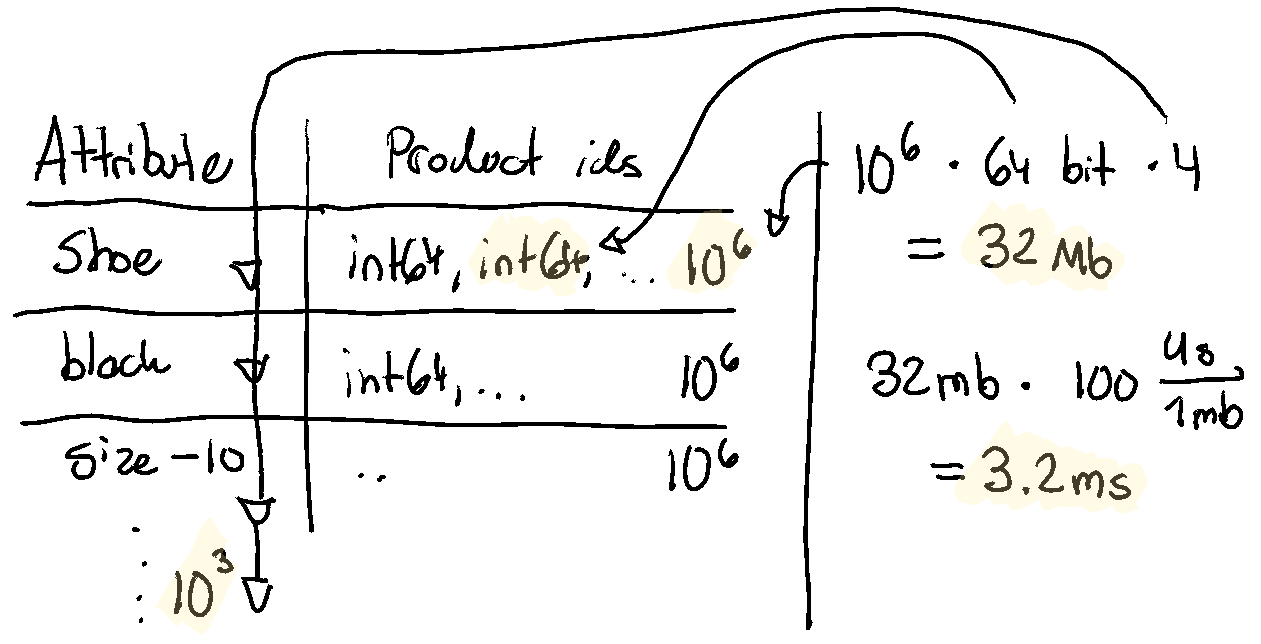
We have 4 bitmaps (one per condition) of 10^6 product ids, each of 64 bits.
That’s 4 * 10^6 * 64 bits = 32 Mb. Would this be in memory or on SSDs? Well,
let’s assume the largest merchants have 10^6 products and 10^3 attributes, that
means a total of 10^6 * 10^3 * 64 bits = 8Gb. That’d cost us about 1 to store on disk. In terms of performance, this is nicely
sequential access. For memory, 32 mb * 100us/mb = 3.2 ms. For SSD (about 10x
cheaper, and 10x slower than memory), 30 ms. 30 ms is a bit high, but 3 ms is
acceptable. $8 is not crazy, given that this would be the absolute largest
merchant we have. If cost becomes an issue, we could likely employ good caching.
You might also like...