Solution to mobile
I assume you have read the task description.
I used about 45 minutes of thinking before I started implementing my first solution to this task. First, I was thinking about doing an actual simulation of expanding the radius of the mobile towers, but I thought that would be very slow, so I abondoned this idea. That was stupid, as seen later. I learned from this task, that sometimes you SHOULD simulate whatever is actually going on!
Because you can have an error margin of Δ10^-3, my first solution was pretty
simple: Start at the very beginning of the road (position p), calculate distances
to all the mobile towers, add 10^-3 to p, repeat for all points. That meant I had to check
from p = 0 to p = l, with the road length l. With
a total n mobile towers, this algorithim ran in `O((1/10^-3) * l
- n) = O(l * n)
time, which was not ideal, sincelgrows pretty quickly as opposed ton`. However, decent for a rather simple solution.
Looking for another solution, I observed that the only relevant points on the road are its endpoints and the intersections between the road, and the line ortogonal on the middle of the line connecting two mobile towers:
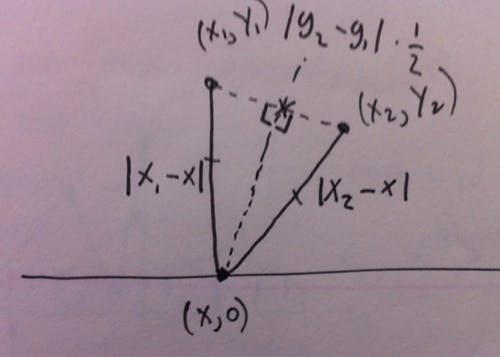
This solution takes O(n^3) time, because you have to check for every single
pair. You can prove that the x-coordinate of these relevant points on the highway for a pair of towers
(x1, y1) and (x2, y2) are calculted by: 1/2 * (x1 + x2 + (y1^2 - y2^2)/(x1 - x2))
I figured I’d be better off with my first solution, which is what I
ended up submitting.
I said that I made the mistake of not simulating the real thing, after the
competition we agreed that the best solution would probably have been exactly
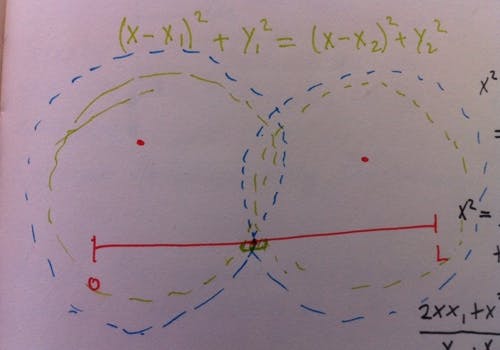
this. If you start with some radius r, and then check whether the circles from
all the towers cover the whole road, you should do a binary search based on the results.
You can check
whether it covers the whole road by finding the intersections between each
circle and the road, then you check whether you can merge these ranges of
intersections in a fashion so that the entire road is covered. This binary
search checks all n towers, thus it runs in O(log(m) * n) time, where m is
the maximum coordinate of a tower.
Not even the binary search is optimum, and you would not receive full points for that solution. Nobody at the competition achieved full points in this task.
You might also like...