Solution to dice

This is an implementation task, which means that it does not require any knowledge of data structures and algorithms other than the trivial. (hashes, arrays, loops, etc.) I assume you have read and understood the task.

This task is considered very easy.

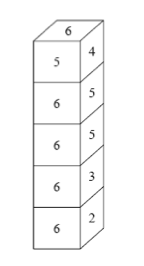
At first I thought this was more of a brute-force problem, but I realized this would take exponential time. With bounds of 1 $<= N <= 10,000$, that would seem rather unlikely. The observation I had to make was that when you have placed the first dice at the bottom, there is only one way the other dice can be stacked on top of the first one. Because the first dice can be rotated in exactly 6 ways, the maximum amount of computations is exactly 6n: Θ(6n). (Just O(n))

While I stacked them in my program, I just find the largest size which is not the one that has to be on top of the previous one, nor the one opposite of that side. I then add each of those numbers to some integer. The largest of those integers, for some rotation of the bottommost dice, is the result: the maximum sum of the sides.

You might also like...

• MySQL transactions per second vs fsyncs per second
• Shitlist Driven Development
• Using checksums to verify syncing 100M database records
• Neural Network From Scratch
• Inverted Index Performance and Merkle Tree Syncronization