Index Merges vs Composite Indexes in Postgres and MySQL

While working with Readwise on optimizing their database for the impending launch of their Reader product, I found myself asking the question: How much faster is a composite index compared to letting the database do an index merge of multiple indexes? Consider this query:

SELECT count(*) /* matches ~100 rows out of 10M */
FROM table
WHERE int1000 = 1 AND int100 = 1
/* int100 rows are 0..99 and int1000 0...9999 */

create table test_table (
  id bigint primary key not null,

  text1 text not null, /* 1 KiB of random data */
  text2 text not null, /* 255 bytes of random data */

  /* cardinality columns */
  int1000 bigint not null, /* ranges 0..999, cardinality: 1000 */
  int100 bigint not null, /* 0..99, card: 100 */
  int10 bigint not null, /* 0..10, card: 10 */
);
/* no indexes yet, we create those in the sections below */

We can create a composite index on (int1000, int100), or we could have two individual indexes on (int1000) and (int100), relying on the database to leverage both indexes.

Having a composite index is faster, but how much faster than the two individual indexes? Let’s do the napkin math, and then test it in PostgreSQL and MySQL.

Napkin Math

We’ll start with the napkin math, and then verify it against Postgres and MySQL.

Composite Index: ~1ms

The ideal index for this count(*) is:

CREATE INDEX ON table (int1000, int100)

It allows the entire count to be performed on this one index.

WHERE int1000 = 1 AND int100 = 1 matches ~100 records of the 10M total for the table. ¹ The database would do a quick search in the index tree to the leaf in the index where both columns are 1, and then scan forward until the condition no longer holds.

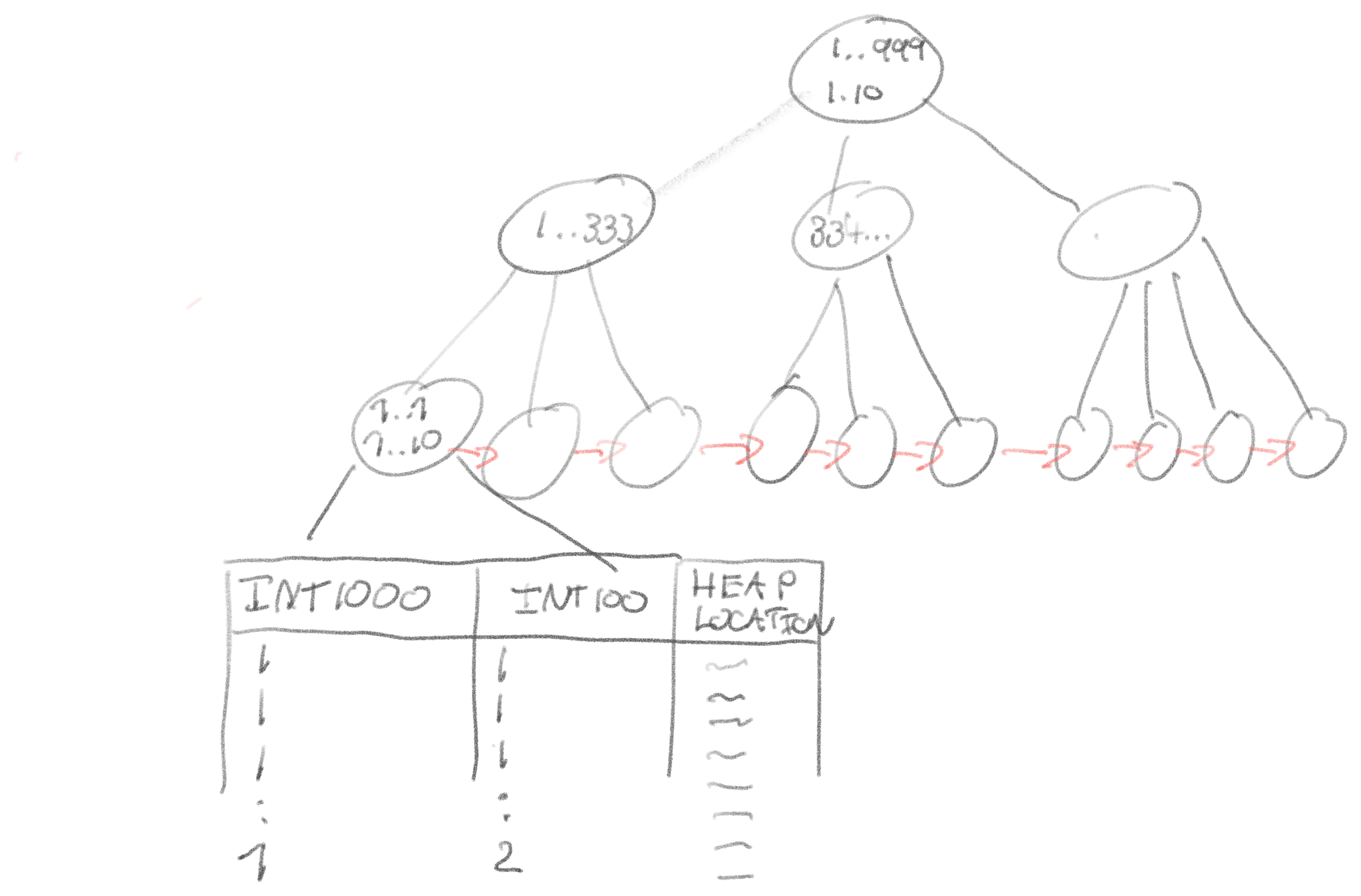
For these 64-bit index entries we’d expect to have to scan only the ~100 entries that match, which is a negligible ~2 KiB. According to the napkin reference, we can read $~1\text{ MiB}/100\text{ μs}$ from memory, so this will take absolutely no time. With the query overhead, navigating the index tree, and everything else, it theoretically shouldn’t take a database more than a couple $100-500 \text{ μs}$ on the composite index to satisfy this query. ²

Index Merge: ~10-30ms

But a database can also do an index merge of two separate indexes:

CREATE INDEX ON table (int1000)
CREATE INDEX ON table (int100)

But how does a database utilize two indexes? And how expensive might this merge be?

How indexes are intersected depends on the database! There are many ways of finding the intersection of two unordered lists: hashing, sorting, sets, KD-trees, bitmap, …

MySQL does what it calls an index merge intersection, I haven’t consulted the source, but most likely it’s sorting. Postgres does index intersection by generating a bitmap after scanning each index, and then ANDing them together.

int100 = 1 returns about $10M \cdot 1/1000 \approx 100,000$ rows, which is about ~1.5 MiB to scan. int1000 = 1 matches only ~10,000 rows, so in total we’re reading about 200 μs worth of memory from both indexes.

After we have the matches from the index, we need to intersect them. In this case, for simplicity of the napkin math, let’s assume we sort the matches from both indexes and then intersect from there.

We can sort $1\text{ MiB}$ in $5\text{ ms}$. So it would take us ~10ms total to sort it, iterate through both sorted lists for a negligible $~200\text{ μs}$ of memory reading, write the intersection to memory for another $~200\text{ us}$, and then we’ve got the interesection, i.e. rows that match both conditions.

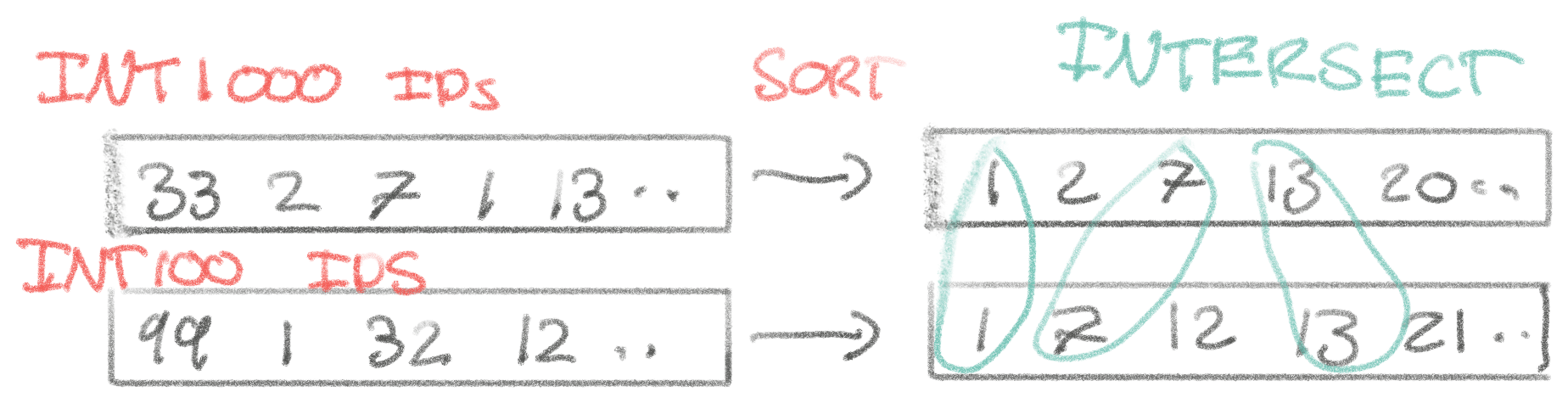
Thus our napkin math indicates that for our two separate indexes we’d expect the query to take $~10\text{ ms}$. The sorting is sensitive to the index size which is fairly approximate, so give it a low multiplier to land at, ~10-30ms.

As we’ve seen, intersection bears a meaningful cost and on paper we expect it to be roughly an order of magnitude slower than composite indexes. However, 10ms is still sensible for most situations, and depending on the situation it might be nice to not have a more specialized composite index for the query! For example, if you are often joining between a subset of 10s of columns.

Reality

Now that we’ve set our expectations from first principles about composite indexes versus merging multiple indexes, let’s see how Postgres and MySQL fare in real-life.

Composite Index: 5ms ✅

Both MySQL and Postgres perform index-only scans after we create the index:

/* 10M rows total, int1000 = 1 matches ~10K, int100 matches ~100K */
CREATE INDEX ON table (int1000, int100)
EXPLAIN ANALYZE SELECT count(*) FROM table WHERE int1000 = 1 AND int100 = 1

/* postgres, index is ~70 MiB */
Aggregate  (cost=6.53..6.54 rows=1 width=8) (actual time=0.919..0.919 rows=1 loops=1)
  ->  Index Only Scan using compound_idx on test_table  (cost=0.43..6.29 rows=93 width=0) (actual time=0.130..0.909 rows=109 loops=1)
        Index Cond: ((int1000 = 1) AND (int100 = 1))
        Heap Fetches: 0

/* mysql, index is ~350 MiB */
-> Aggregate: count(0)  (cost=18.45 rows=1) (actual time=0.181..0.181 rows=1 loops=1)
    -> Covering index lookup on test_table using compound_idx (int1000=1, int100=1)  (cost=9.85 rows=86) (actual time=0.129..0.151 rows=86 loops=1)

They each take about ~3-5ms when the index is cached. It is a bit slower than the ~1ms we expected from the napkin math, but in our experience working with napkin math on database, tracks within an order of magnitude to seem acceptable. We attribute this to overhead of walking through the index. ³

Index Merge

MySQL: 30-40ms ✅

When we execute the query in MySQL it takes ~30-40ms, which tracks well the upper end of our napkin math. That means our first principle understanding likely lines up with reality!

Let’s confirm it’s doing what we expect by looking at the query plan:

/* 10M rows total, int1000 = 1 matches ~10K, int100 matches ~100K */
EXPLAIN ANALYZE SELECT count(*) FROM table WHERE int1000 = 1 AND int100 = 1

/* mysql, each index is ~240 MiB */
-> Aggregate: count(0)  (cost=510.64 rows=1) (actual time=31.908..31.909 rows=1 loops=1)
    -> Filter: ((test_table.int100 = 1) and (test_table.int1000 = 1))  (cost=469.74 rows=409) (actual time=5.471..31.858 rows=86 loops=1)
        -> Intersect rows sorted by row ID  (cost=469.74 rows=410) (actual time=5.464..31.825 rows=86 loops=1)
            -> Index range scan on test_table using int1000 over (int1000 = 1)  (cost=37.05 rows=18508) (actual time=0.271..2.544 rows=9978 loops=1)
            -> Index range scan on test_table using int100 over (int100 = 1)  (cost=391.79 rows=202002) (actual time=0.324..24.405 rows=99814 loops=1)
/* ~30 ms */

MySQL’s query plan tells us it’s doing exactly as we expected: get the matching entries from each index, intersecting them and performing the count on the intersection. Running EXPLAIN without analyze I could confirm that it’s serving everything from the index and never going to seek the full row.

Postgres: 25-90ms 🤔

Postgres is also within an order of magnitude of our napkin math, but it’s on the higher range with more variance, in general performing worse than MySQL. Is its bitmap-based intersection just slower on this query? Or is it doing something completely different than MySQL?

Let’s look at the query plan using the same query as we used from MySQL:

/* 10M rows total, int1000 = 1 matches ~10K, int100 matches ~100K */
EXPLAIN ANALYZE SELECT count(*) FROM table WHERE int1000 = 1 AND int100 = 1

/* postgres, each index is ~70 MiB */
Aggregate  (cost=1536.79..1536.80 rows=1 width=8) (actual time=29.675..29.677 rows=1 loops=1)
  ->  Bitmap Heap Scan on test_table  (cost=1157.28..1536.55 rows=95 width=0) (actual time=27.567..29.663 rows=109 loops=1)
        Recheck Cond: ((int1000 = 1) AND (int100 = 1))
        Heap Blocks: exact=109
        ->  BitmapAnd  (cost=1157.28..1157.28 rows=95 width=0) (actual time=27.209..27.210 rows=0 loops=1)
              ->  Bitmap Index Scan on int1000_idx  (cost=0.00..111.05 rows=9948 width=0) (actual time=2.994..2.995 rows=10063 loops=1)
                    Index Cond: (int1000 = 1)
              ->  Bitmap Index Scan on int100_idx  (cost=0.00..1045.94 rows=95667 width=0) (actual time=23.757..23.757 rows=100038 loops=1)
                    Index Cond: (int100 = 1)
Planning Time: 0.138 ms

/* ~30-90ms */

The query plan confirms that it’s using the bitmap intersection strategy for intersecting the two indexes. But that’s not what’s causing the performance difference.

While MySQL services the entire aggregate (count(*)) from the index, Postgres actually goes to the heap to get every row. The heap contains the entire row, which is upwards of 1 KiB. This is expensive, and when the heap cache isn’t warm, the query takes almost 100ms! ⁴

As we can tell from the query plan, it seems that Postgres is unable to do index-only scans in conjunction with index intersection. Maybe in a future Postgres version they will support this; I don’t see any fundamental reason why they couldn’t!

Going to the heap doesn’t have a huge impact when we’re only going to the heap for 100 records, especially when it’s cached. However, if we change the condition to WHERE int10 = 1 and int100 = 1, for a total of 10,000 matches, then this query takes 7s on Postgres, versus 200ms in MySQL where the index-only scan is alive and kicking!

So MySQL is superior on index merges where there is an opportunity to service the entire query from the index. It is worth pointing out though that Postgres’ lower-bound when everything is cached is lower for this particular intersection size, likely its bitmap-based intersection is faster.

Postgres and MySQL do have roughly equivalent performance on index-only scans though. For example, if we do int10 = 1 Postgres will do its own index-only scan because only one index is involved.

The first time I ran Postgres for this index-only scan it was taking over a second, I had to run VACUUM for the performance to match! Index-only scans require frequent VACUUM on the table to avoid going to the heap to fetch the entire row in Postgres.

VACUUM helps because Postgres has to visit the heap for any records that have been touched since the last VACUUM, due to its MVCC implementation. In my experience, this can have serious consequences in production for index-only scans if you have an update-heavy table where VACUUM is expensive.

Conclusion

Index merges are ~10x slower than composite indexes because the ad-hoc intersection isn’t a very fast operation. It requires e.g. sorting of the output of each index scan to resolve. Indexes could be optimized further for intersection, but this would likely have other ramifications for steady-state load.

If you’re wondering if you need to add a composite index, or can get away with creating to single indexes and rely on the database to use both indexes — then the rule of thumb we establish is that an index merge will be ~10x slower than the composite index. However, we’re still talking less than 100ms in most cases, as long as you’re operating on 100s of rows (which in a relational, operational database, hopefully you mostly are).

The gap in performance will widen when intersecting more than two columns, and with a larger intersection size—I had to limit the scope of this article somewhere. Roughly an order of magnitude seems like a reasonable assumption, with ~100 rows matching many real-life query averages.

If you are using Postgres, be careful relying on index merging! Postgres doesn’t do index-only scans after an index merge, requiring going to the heap for potentially 100,000s of records for a count(*). If you’re only returning 10s to 100s of rows, that’s usually fine.

Another second-order take-away: If you’re in a situation where you have 10s of columns filtering in all kinds of combinations, with queries like this:

SELECT id
FROM products
WHERE color=blue AND type=sneaker AND activity=training 
  AND season=summer AND inventory > 0 AND price <= 200 AND price >= 100
  /* and potentially many, many more rules */

Then you’re in a bit more of a pickle with Postgres/MySQL. It would require a combinatoric explosion of composite indexes to support this use-case well, which would be critical for sub 10ms performance required for fast websites. This is simply unpractical.

Unfortunately, for sub 10ms response times, we also can’t rely on index merges being that fast, because of the ad-hoc interesection. I wrote an article about solving the problem of queries that have lots of conditions with Lucene, which is very good at doing lots of intersections. It would be interesting to try this with GIN-indexes (inverted index, similar to what Lucene does) in Postgres as a comparison. Bloom-indexes may also be suited for this. Columnar database might also be better at this, but I haven’t looked at that in-depth yet.